گاسپار مونژ در سال 1746 در شهر کوچک بون واقع در فرانسه متولد شد. مونژ که فرزند کاسب دوره گردی بود در 16 سالگی به تیزکردن چاقو و قیچی و غیره می پرداخت وی با وسایلی که به دست خود ساخته بود نقشه بزرگی از وطن خود تهیه کرد که مورد توجه و تحسین فراوان واقع شد و نقشه او را در فرمانداری نصب کردند.

معلمین او پس از مشاهده نقشه گفتند او داناتر از آن است که شاگرد ما باشد و او را برای تدریس فیزیک به مدرسه کشیشان شهر لیون فرستادند وی دستیار شارل بوسو، استاد ریاضیات، شد در سال 1768 مونژ جانشین او شد اگر چه مقام استادی نداشت سال بعد به عنوان مدرس فیزیک تجربی در مدرسه جای آبه نوله را گرفت

در این سمتهای دو گانه که قسمتی از آن اختصاص به هدفهای علمی داشت مونژ نشان داد که ریاضیدان و فیزیکدانی توانا، طراحی با استعداد، آزمایگشری ماهر و معلمی در تراز اول است. مونژ به مطلعه بعضی از شاخه های هندسه دوباره جان بخشید و کار وی نقطه شروع شکوفایی فوق العاده آن رشته در سده 19 بود علاوه بر این پژوهشهای وی به رشته های دیگر تحلیل ریاضی کشیده شد خصوصاٌ به نظریه معادلات دیفرانسیل جزئی و مسائل فیزیک، شیمی و فناوری. مونژ که معلمی نامدار و رئیس مدرسه ای بی نظیر بود، مسئولیتهای مهم اداری و سیاسی را در طول انقلاب و دوره امپراطوری بر عهده گرفت بنابراین وی یکی از مبتکرترین ریاضیدانان عصر خود بود مونژ خیلی زود کارهای شخصی خود را آغاز کرد پژوهشهای وره جوانی او(1766 – 1772) بسیار متنوع اما جلوه دهنده خصوصیاتی بودند که نشانه استعداد کامل وی بود: از جمله حس تند و تیز درک واقعیت هندسی، علاقه به مسائل علمی، توانایی عظیم تحلیلی و توجه به جنبه های متعدد تحلیلی هندسی. در جریان سالهای 1777 تا 1780 مونژ عمدتاٌ به فیزیک و شیمی علاقه مند بود و مقدمات تهیه آزمایشگاه شیمی مجهزی را برای مدرسه مهندسی فراهم آورد انتخاب شدنش به عضویت فرهنگستان علوم به عنوان هندسه دان دستیار در سال 1780 زندگی مونژ را دگرگون ساخت زیرا وی را مجبور کرد که بر اساس منظمی در پاریس اقامت کند در پاریس در طرحهای فرهنگستان شرکت کرد و مقاله هایی در باره فیزیک و شیمی و ریاضیات تنظیم و عرضه نمود فهرستی از مطالبی که به فرهنگستان تقدیم کرد گواه بر تنوع آنها است: ترکیب اسید نیتریک، ا=تولید سطوح منحنی، معادلات تفاضلی متناهی و معادلات دیفرانسیل جزئی، انعکاس مضاعف و ساختار اسپات اسبند، ترکیب آهن، فولاد و چدن و تاثیر جرقه های برقی و بر گاز بیو کسید کربن، پدیده موئینگی و علل بعضی از پدیده های هواشناختی و بررسی در نور شناسی فیزولوژیک.

وقتی انقلاب در 1789 آغاز شد مونژ در زمره شناخته شده ترین دانشمندان فرانسوی بود او که عضو بسیار فعال فرهنگستان علوم بود شهرتی در ریاضیات و فیزیک و شیمی کسب کرده بود به عنوان ممتحن دانشجویان افسری نیروی دریایی، شاخه ای از مدارس نظامی فرانسه را رهبری می کرد که در آن زمان عملاٌ تنها مؤسسات نظامی بودند که تعلیمات علمی شایسته ای به دانشجویان خود می دادند و این مقام وی را، در هر بندری که از آن دیدار می کرد با دیوانسالارانی در تماس می گذاشت که اندکی بعد تحت مدیریت او قرار می گرفتند این مقام همچنین وی را قادر ساخت که معدنهای آهن، کارخانه ذوب آهن و کارخانه های دیگر را ببیند و بدین ترتیب در کار فلز پردازی و مسائل فناوری خبره و صاحب نظر شود علاوه بر این اصلاح مهمی که در 1776 در روش تعلیم در مدارس نیروی دریایی انجام داده بود وی را برای تلاشهایی آماده ساخت کهدر زمان انقلاب برای تازه کردن روشهای علمی و فنی بر عهده گرفت در سال 1794 مسئولیت تاسیس مدرسه مرکزی کارهای عامه(که بعداٌ به مدرسه پلی تکنیک تبدیل شد) به وی محول گردید مونژ مه در سال 1794 به عنوان معلم هندسه ترسیمی منصوب شد بر عمل تربیت سرکارگران آینده نظارت کرد و هندسه ترسیمی را در دوره های انقلابی که برای تکمیل تربیت دانشجویان آینده طراحی شده بودند تدریس نمود و یکی از فعالترین عضوهای شورای مدیریت بود. این مدرسه پس از دو ماه تاخیر که بر اثر مشکلات سیاسی پیش آمد در سال 1795 به نجومی منظم شروع به کار کرد. هر چند وظایفی که به عنوان سناتور به عهده مونژ محول شد موجب گردید که او چند بار از درسهایش در مدرسه پلی تکنیک دور شود از علاقه شدیدش به مدرسه هیچ کاسته نشد مراقبت دقیق در پیشرفت دانشجویان داشت و کارهای پژوهشی انان را دنبال می کرد و دقت خاصی به برنامه تعلیمات مبذول داشت بیشتر آنچه مونژ در این دوره منتشر کرد برای دانشجویان مدرسه پلی تکنیک نوشته شده بود موفقیت گسترده کتاب او بنام«هندسه ترسیمی) (1799) باعث اشاعه سریع این شاخه جدید هندسه هم در فرانسه و هم در خارج از آن شد. این اثر چند بار چاپ شد.

کار عملی مونژ ریاضیات(شاخه های گوناگون هندسه و تحلیل ریاضی) فیزیک، مکانیک و نظریه ماشینها را در می گرفت اگر چه اطلاع از جزئیات خدمات مونژ به فیزیک بسیار ناچیز است زیرا وی هرگز اثر عمده ای در این زمینه منتشر نساخت خدمات اصلی وی متمرکز بودند بر نظریه آزمایش‌های مربوط به گرما، صوت، برق ساکن، نور شناسی(نظریه سرابها) مهمترین پژوهش مونژ در شیمی مربوط بود به ترکیب آب. خیلی زود، در سال 1781 وی ترکیب اکسیژن با ئیدروژن را در لوله اکسیژن سنج تحقق بخشید و در سال 1783 – همزمان با لاووازیه و بی ارتباط با او – آب را ترکیب کرد. با این که اسباب مونژ بسیار ساده تر بود نتایج اندازه گیریهایش دقیقتر بودند. در قلمرو تجربی در سال 1784 مونژ با همکاری کلوله برای نخسین بار موفق شد که گازی را مایع سازد و آن انیدرید سولفور(بیوکسیدگوگرد) بود.

سراجام بین سالهای 1786 و 1788 مونژ با برتوله و اندر مونه در اصول فلز پردازی و ترکیب آهن و چدن و فولاد به پژوهش پرداخت. مونژ مردی شجاع و از دوستان ناپلئون بود و در سال 1798 به اتفاق او به کشور مصر رفت در این سفر ناپلئون نتوانست او را از شرکت در حمله به اسکندریه منصرف سازد.

بعد از آنکه ناپلئون روانه سنت هلن گردید مخترع هندسه ترسیمی و ایجاد کننده اصلی مدرسه پلی تکنیک هم تمام عناوین خود را از دست داد و از آکادمی رانده شد. مونژ در 28 سال 1818 در 72 سالگی در پاریش درگذشت مخترع هندسه ترسیمی میراثی عظیم از خود به جا گذاشت زیرا ساختن ماشینهای مدرن و عمارات عظیم بدون کمک آن ممکن نیست.

بلزپاسکال»

 «بلزپاسکال» ریاضیدان، و فیزیکدان، و فیلسوف بزرگ فرانسوی، در قرن 17زندگی می‌کرد. او ماشین حساب را ساخته است. و نیز نشانه‌های کلی بخش پذیری هر عدد صحیح به هر عدد صحیح دیگر را پیدا کرده است. و نیز یک مثلث عددی خاصی ترتیب داده است، که به نام خود او «مثلث پاسکال» نامیده می‌شود. و منظور ما در اینجا آشنایی با همین مثلث است. اما قبل ازاینکه مثلث پاسکال را توضیح دهیم، ناچاریم ابتدا دو عدد مخصوص را بشناسیم:

اولا ّعدد مثلثی چیست؟ این عدد حاصل جمع چند جمله‌ی متوالی یک تصاعد عددی است، که جمله‌ی اول آن 1وقدرنسبتش عددصحیح است. مثلاّ در تصاعد عددی7، 6، 5، 4، 3 ، 2، 1اعداد(1) و (2+1) و (3+2+1)و (4+3+2+1)...و یعنی عددهای 1و3و6و10و15و...را اعداد مثلثی می‌نامند، زیرا با هر یک از آنها می‌توان تشکیل مثلث متساوی‌الاضلاع داد. مثلاّ اگر6 گلوله‌ی را در ردیفهای 1و2و3تایی کنار هم روی میز قرار دهید، یک مثلث متساوی‌الاضلاع تشکیل می‌شود. حال اگر4گلوله‌ی شیشه‌ای دیگر را زیر آنها قرار داده، و ردیف جدید را تشکیل دهید، یک مثلث متساوی‌الاضلاعجدید شامل 10گلوله خواهید‌داشت.

ثانیاّ عدد هرمی چیست؟ گفتیم که با10گلوله‌ی شیشه‌ای می‌توان یک مثلث منتظم تشکیل داد. مثلث قشر دوم را که با6گلوله ساخته می‌شود، و روی آن قرار‌داد. و سرانجام یک گلوله‌ی شیشه‌ای را هم می‌توان روی آنها گذاشت، و با چهار ردیف مثلث، که از گلوله‌های شیشه‌ای تشکیل یافته‌اند، که یک عدد مثلثی بلافاصله بزرگتر زیر آنها بگذاریم، پس با معلوم بودن سری اعداد مثلثی 1و3و6و10و 15و 21و 28و36و 45و 55 و... ساختن اعداد هرمی آسان است: از1 شروع می‌کنیم، مرتباّ تا هر جا که بخواهیم، با عددهای مثلثی پشت سرخود جمع می‌کنیم، تا پشت سرهم عددهای هرمی حاصل شوند. مثلاّ از مجموع 1و3و6و10و15و21عدد56 به دست می‌آید، که یک عدد هرمی است.

عکس پیدا نشد

و برای پیدا‌کردن عدد هرمی بزرگتر از آن باید روی 56 عدد28را بیفزاییم تا84 به دست‌آید. و حالا مثلث پاسکال: مثلث‌پاسکال به این ترتیب درست شده است، که هرعدد (جز‌واحدهای کنار آن) از مجموع نزدیکترین دو‌عدد بالای آن درست شده است. مثلاّ120حاصل جمع عددهای 84 و36 است، که در ردیف افقی فوقانی آن، و در طرفین عدد مزبور قرار دارند. در این جدول شگفت‌انگیز نخستین ردیف اریب را واحدها تشکیل داده‌اند. در دومین ردیف اریب سری عددهای طبیعی قرار دارند. در سومین ردیف اریب اعداد مثلثی پشت سر هم واقع شده اند. و در چهارمین ردیف اریب عددهای هرمی1و4و10و20و35و56 و... به دنبال هم قرار گرفته‌اند.برای اطلاع از ویژگیهای ردیف اریب باید به فضای چهار بعدی برویم، که فعلاّ از آن صرفنظر می‌کنیم.

شما می‌توانید بین اعداد واقع در این مثلث ویژگیهای عجیب دیگری هم کشف کنید مثلاّ اعداد «فیبوناچی» هم در مثلث پاسکال ظاهر می‌شوند، که گویا خود پاسکال از آن بی‌اطلاع بوده است. در واقع این ویژگی مثلث پاسکال تا نیمه‌ی دوم قرن نوزدهم ناشناخته بود.
برای به دست آوردن اعداد فیبوناچی از مثلث‌پاسکال، کافی است به خطوط اریبی، که بالای این مثلث به موازات هم رسم کرده ایم، توجه کنید.

عکس پیدا نشد

خواهید‌دید که مجموع عددهای واقع در هر ردیف به ترتیب اعداد فیوناچی را می‌رساند. و شما می‌توانید رسم خطهای اریب را زیرهم ادامه دهید، و مجموع اعداد واقع در روی آنها را به دست آورید، تا سری اعداد فیبوناچی کامل شوند.
از خصوصیات جالب مثلث‌پاسکال این است که مجموع عددها در هر سطر افقی برابر است با توانی از2، مثلاّ اعداد واقع در پنجمین ردیف افقی را اگرجمع کنیم، 16می شود، که برابر24است. و مجموع اعداد ششمین ردیف افقی نیز 32 یا 25است.
و حالا نوبت شماست، که اعداد واقع در این مثلث را به دقت مورد بررسی قرار‌دهید، تا ویژگیهای جدیدی در آن کشف کنید.

اراتستن

 اولین فردی که اندازه زمین را دقیق اندازه گرفت، اراتستن (195 ـ 276 قبل از میلاد) ریاضیدان یونانی بود. او می دانست که درظهر اواسط تابستان خورشید در شهر سین، واقع در جنوب خانه اش در اسکندریه مصر، مستقیما درون چاه عمیقی می تابد. او در همان روز زاویه تابش خورشید بر فراز اسکندریه را 2/7 درجه اندازه گرفت. این زاویه برابر است با یک پنجاهم کمان یک دایره. او می دانست که فاصله سین و اسکندریه 772 کیلومتر است و بدین ترتیب محیط زمین را 772×50 یعنی 38600 کیلومتر محاسبه کرد. این رقم به عدد واقعی 40074 کیلومتر بسیار نزدیک است.

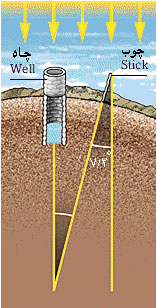اندازه گیری دقیق اراتستن با سایه یک چوب زاویه تابش خورشید در اسکندریه را محاسبه کرد.