![]()
 استفاده می شود. لذا می توان گفت:
استفاده می شود. لذا می توان گفت: 
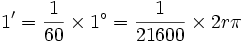
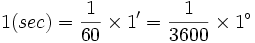
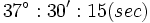



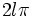 است. یک رادیان اندازه زاویه مرکزی مقابل به کمانی از دایره است که طول کمان روبرو به آن برابر شعاع دایره است.
است. یک رادیان اندازه زاویه مرکزی مقابل به کمانی از دایره است که طول کمان روبرو به آن برابر شعاع دایره است.  رادیان است و زاویه نیم صفحه برابر
رادیان است و زاویه نیم صفحه برابر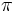 رادیان است. و لذا:
رادیان است. و لذا:  که در آن P محیط دایره است.
که در آن P محیط دایره است.  برابر s و شعاع دایره r باشد آنگاه اندازه زاویه تتا بر حسب رادیان را می توان با یک تناسب ساده چنین محاسبه کرد:
برابر s و شعاع دایره r باشد آنگاه اندازه زاویه تتا بر حسب رادیان را می توان با یک تناسب ساده چنین محاسبه کرد: 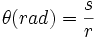
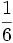 محیط دایره است چند رادیان است؟
محیط دایره است چند رادیان است؟ 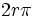 باشد آنگاه اندازه زاویه برابر است با
باشد آنگاه اندازه زاویه برابر است با  رادیان حال اگر
رادیان حال اگر 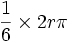 باشد اندازه زاویه چقدر می شود؟
باشد اندازه زاویه چقدر می شود؟ 
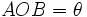 را در دایره در نظر بگیرید:
را در دایره در نظر بگیرید:  برحسب درجه D، برحسب گراد G و برحسب رادیان R باشد. با استفاده از تناسب داریم:
برحسب درجه D، برحسب گراد G و برحسب رادیان R باشد. با استفاده از تناسب داریم: | طول کمان | اندازه زاویه برحسب درجه |
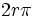 |
360 |
 |
D |
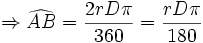
| طول کمان | اندازه کمان برحسب گراد |
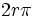 |
400 |
 |
G |
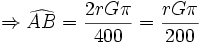
| طول کمان | اندازه زاویه برحسب رادیان |
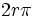 |
 |
 |
R |
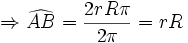
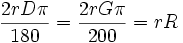

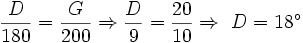
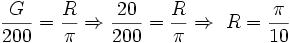

 را تند یا حاده میگوییم هرگاه اندازه اش کمتر از 90 در جه باشد. به عبارت دیگر:
را تند یا حاده میگوییم هرگاه اندازه اش کمتر از 90 در جه باشد. به عبارت دیگر: 
 را راست یا قائم میگوییم هرگاه اندازه آن برابر 90 در جه باشد. به عبارت دیگر:
را راست یا قائم میگوییم هرگاه اندازه آن برابر 90 در جه باشد. به عبارت دیگر: 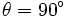
 را باز یا منفرجه می گوییم هرگاه بزرگتر از 90 درجه و کمتر از 180 درجه باشد. به عبارت دیگر:
را باز یا منفرجه می گوییم هرگاه بزرگتر از 90 درجه و کمتر از 180 درجه باشد. به عبارت دیگر:
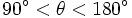
 را نیم صفحه میگوییم هرگاه برابر 180 درجه باشد. به عبارت دیگر:
را نیم صفحه میگوییم هرگاه برابر 180 درجه باشد. به عبارت دیگر: 
 را زاویه بازتاب میگوییم هرگاه بزرگتر از 180 درجه و کمتر از 360 درجه باشد. به عبارت دیگر:
را زاویه بازتاب میگوییم هرگاه بزرگتر از 180 درجه و کمتر از 360 درجه باشد. به عبارت دیگر:
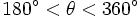
 زاویه را کامل یا ت
زاویه را کامل یا ت مام صفحه می گوییم هرگاه برابر 360 درجه باشد. به عبارت دیگر:.
مام صفحه می گوییم هرگاه برابر 360 درجه باشد. به عبارت دیگر:. 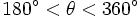
 را کامل یا تمام صفحه می گوییم هرگاه برابر 360 درجه باشد. به عبارت دیگر:
را کامل یا تمام صفحه می گوییم هرگاه برابر 360 درجه باشد. به عبارت دیگر: .
. 