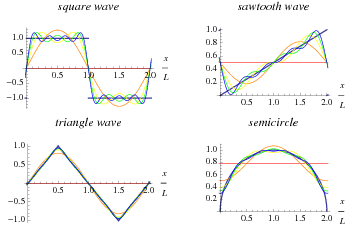
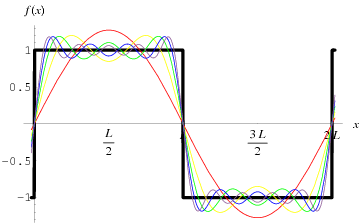
سری فوریه عبارت است از بسط تابع تناوبی 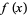 در قالب جملاتی از جمع نامتناهی کسینوس ها و سینوس ها. در واقع سری فوریه بر کاربرد روابط تعامد (orthogonality relationships) توابع سینوسی و کسینوسی تاکید دارد. محاسبه و مطالعه ی سری های فوریه موسوم به آنالیز هارمونیک (harmonic analysis) می باشد که به عنوان یک روش بسیار سودمند برای تفکیک یک تابع تناوبی دلخواه به مجموعه ای از جملات ساده بوده که به راحتی می توان آنها را فهمید، منحصرا حل کرد و دوباره با ترکیب آنها راه حل مساله ی اولیه را بدست آورد، یا اینکه یک تقریب مطلوب و مناسبی را برای آن تخمین زد. نمونه هایی از تقریب های متوالی برای توابع معمول در ریاضیات با استفاده از سری های فوریه در شکل بالا گرداوری شده است.

به ویژه از آن جایی که با توجه به اصل انطباق (برهم نهی) مجموع پاسخ های یک معادله ی دیفرانسیلی معمولی همگن خطی خود راه حل معادله ی اولیه محسوب می شوند، چنانچه بک چنین معادله ای را بتوان برای یک خم سینوسی یکتا حل کرد، آنگاه راه حل یک تابع دلخواه را می توان فورا با استفاده از توصیف تابع اولیه در قالب یک سری فوریه بدست آورد که متعاقبا این رویه منجر به فهم راه حل هر یک از مولفه های منتسب به خم سینوسی می گردد. این تکنیک حتی در برخی موارد خاص که سری فوریه محصور به یک شکل محدود و بسته است، به راه حل های تحلیلی نیز می انجامد.

هر مجموعه ای از توابعی که یک دستگاه متعامد (راست گوشه) کامل (complete orthogonal system) را تشکیل می دهند، یک سری فوریه ی تعمیم یافته (generalized Fourier series) متناظر دارند که شبیه به سری فوریه است. مثلاْ استفاده از تعامد ریشه های تابع بسل نوع اول (Bessel function of the first kind) به اصطلاح یک سری بسل ـ فوریه (Bessel function of the first kind) را بدست می دهد.

محاسبه ی سری فوریه (معمول) بر پایه ی اتحاد های انتگرالی زیر است:

که  و  نماد دلتای کرونکر است:

با استفاده از متد سری فوریه تعمیم یافته (generalized Fourier series) سری فوریه ی معمول شامل جملات سینوسی و کسینوسی با قرار دادن  و  حاصل می شود. چون این توابع یک دستگاه متعامد کامل در بازه ی را ایجاد می کنند، سری فوریه تابع 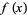 به صورت زیر داده می شود:

که

 و ... n=1،2،3 توجه کنید که عامل a₀ در فرم خاصی نوشته شده است که در قیاس با شکل عمومی سری فوریه تعمیم یافته می تواند تقارن نسبت به تعاریف  a_n و b_n را حفظ کند.

اگر یک تابع شرایط دیریشله (Dirichlet conditions) را تصدیق کند، سری فوریه تابع مزبور همگرا به تابع  می باشد که برابر با تابع اولیه در نقاط پیوستگی و یا میانگین دو حد در نقاط ناپیوستگی است، یعنی

 x_0^-)f(x)+lim_(x->x_0^+)f(x)] for -pi-pi^+)f(x)+lim_(x->pi_-)f(x)] for x_0=-pi,pi " src="http://mathworld.wolfram.com/images/equations/FourierSeries/NumberedEquation2.gif" width=290 border=0>